Gauss- Seidel elimination
Posted by Jonathan Celis
Now i have a new topic to talk about and its Gauss-Seidel method, i find it very interesting so im going to explain it here.
After reading this, you should be able to:
1. solve a set of equations using the Gauss-Seidel method,
2. recognize the advantages and pitfalls of the Gauss-Seidel method, and
3. determine under what conditions the Gauss-Seidel method always converges.
Why do we need another method to solve a set of simultaneous linear equations?
In certain cases, such as when a system of equations is large, iterative methods of solving equations are more advantageous. Elimination methods, such as Gaussian elimination, are prone to large round-off errors for a large set of equations. Iterative methods, such as the Gauss-Seidel method, give the user control of the round-off error. Also, if the physics of the problem are well known, initial guesses needed in iterative methods can be made more judiciously leading to faster convergence.
What is the algorithm for the Gauss-Seidel method? Given a general set of equations and unknowns, we have

If the diagonal elements are non-zero, each equation is rewritten for the corresponding unknown, that is, the first equation is rewritten with on the left hand side, the second equation is rewritten with on the left hand side and so on as follows
so
As i always say, it is important to make an example so the concepts get clear, and here it is:
Example
Find the solution to the following system of equations using the Gauss-Seidel method.
Use
as the initial guess and conduct two iterations.
Solution
The coefficient matrix
is diagonally dominant an the inequality is strictly greater than for at least one row. Hence, the solution should converge using the Gauss-Seidel method.
Rewriting the equations, we get
Iteration #1
The absolute relative approximate error at the end of the first iteration is
Iteration #2
At the end of second iteration, the absolute relative approximate error is:
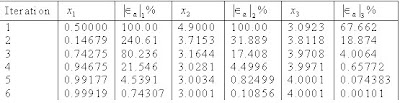
This is close to the exact solution vector of 

